<프로그래머스> 크레인 인형뽑기

문제링크

https://programmers.co.kr/learn/courses/30/lessons/64061

문제 분석

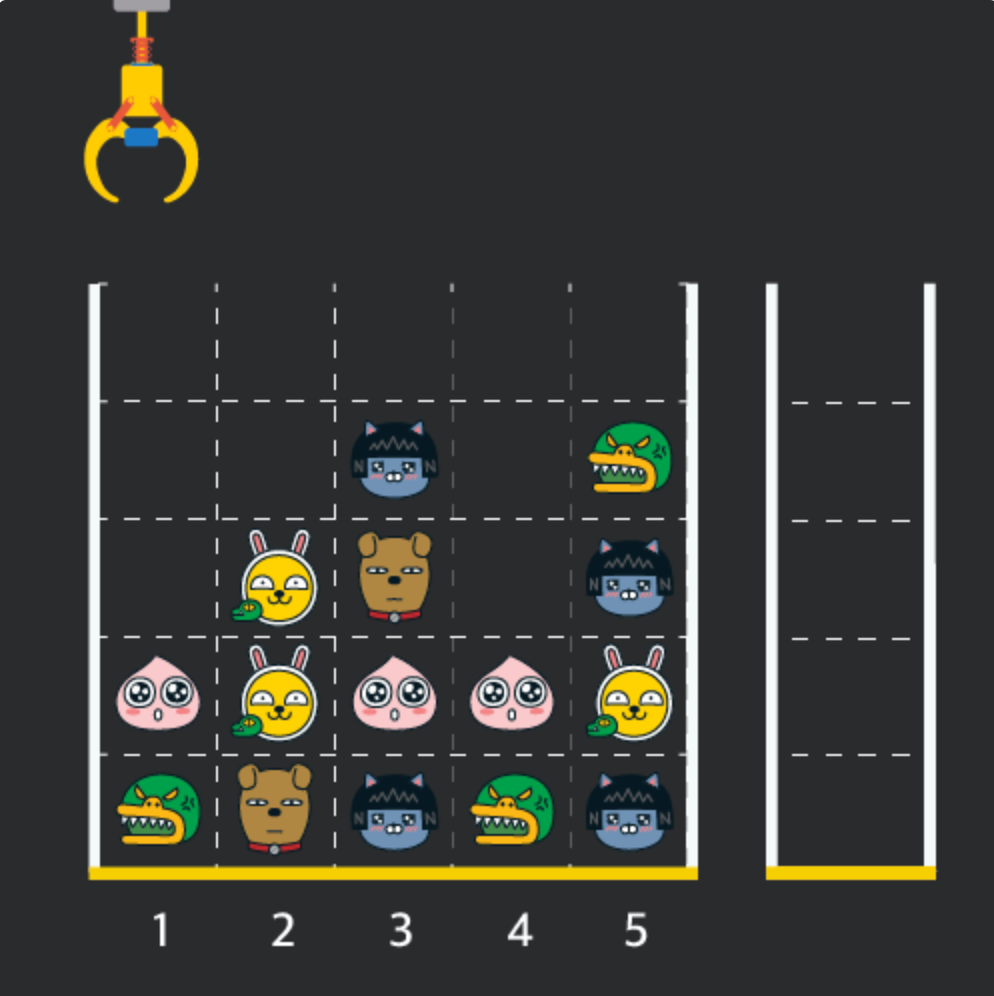
• 주어지는 2차원 배열(board)은 아래의 그림처럼 인형뽑기 판을 나타낸다.
• moves배열의 경우, 집게가 아래의 숫자 중 어디로 갈지 결정하는 배열인데, 해당 배열은 시작 index를 1로 잡았기에 구현시 move - 1의 값을 board에 넣어서 구현해야한다.
• 접근할 열을 지정후(move-1이 board에서 접근해야 할 열의 인덱스를 나타냄), 해당 열을 내려가면서 0이 아닌값을 만나면 해당값을 스택에 푸쉬한다.
• 이후 스택에 연속적으로 같은 값이 생기면 double pop을 해서 연속되는 값  두개를 없애고, 카운팅을 1 증가시킨다.
• 최종적으로 카운팅 된 숫자가 정답이 된다.

구현 코드

import java.util.Stack;

public class CrainGame {
    public static int solution(int[][] board, int[] moves) {
        int answer = 0;
        Stack<Integer> res_stack = new Stack<>();//결과를 반영할 스택, 인형을 뽑은 후 인형을 쌓는 스택이라고 이해하기 
        int peek_value = -1;
        int count = 0;
        int row = 0;
        int col = 0;
        /*
            move를 증가 시켜가면서 몇번째 열로 접근 할지를 결정한다.
            Line 18 : 만약 보드의 숫자가 0이 아니라면, 즉 숫자가 들어가 있다 == 인형이 존재하면,
            res_stack에 해당 값을 푸쉬하고 해당 스택을 peek()해서 연속으로 같은수가 두번 들어가는 체크한다.
        */
        for (int move : moves) {
            for (int j = 0; j < board.length; j++) {
                if(board[j][move - 1] != 0){
                    res_stack.push(board[j][move - 1]);
                    if (peek_value == res_stack.peek()) {
                        doublePop(res_stack);
                        count++;
                    }
                    if(res_stack.size() == 0){
                        peek_value = -1;
                    }else{
                        peek_value = res_stack.peek();
                    }
                    row = j;
                    col = move - 1;
                    break;
                }
            }
            board[row][col] = 0; //인형을 꺼낸 인덱스의 값을 0으로 설정
        }
        answer = 2 * count;
        return answer;
    }

    public static void doublePop(Stack<Integer> stack){
        stack.pop();
        stack.pop();
    }

    public static void main(String[] args) {
        System.out.println(solution(new int [][]{{0,0,1,0,0},{0,0,1,0,0},{0,2,1,0,0},{0,2,1,0,0},{0,2,1,0,0}},new int [] {1,2,3,3,2,3,1}));

    }
}